III. Search Space

Search Space

If we are solving some problem, we are usually looking for some solution, which will be the best among others. The space of all feasible solutions (it means objects among those the desired solution is) is called search space (also state space). Each point in the search space represent one feasible solution. Each feasible solution can be "marked" by its value or fitness for the problem. We are looking for our solution, which is one point (or more) among feasible solutions - that is one point in the search space.

The looking for a solution is then equal to a looking for some extreme (minimum or maximum) in the search space. The search space can be whole known by the time of solving a problem, but usually we know only a few points from it and we are generating other points as the process of finding solution continues.

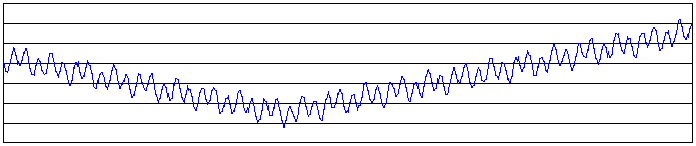
space

Example of a search space

The problem is that the search can be very complicated. One does not know where to look for the solution and where to start. There are many methods, how to find some suitable solution (ie. not necessarily the best solution), for example hill climbing, tabu search, simulated annealing and genetic algorithm. The solution found by this methods is often considered as a good solution, because it is not often possible to prove what is the real optimum.

NP-hard Problems

Example of difficult problems, which cannot be solved int "traditional" way, are NP problems.

There are many tasks for which we know fast (polynomial) algorithms. There are also some problems that are not possible to be solved algorithmicaly. For some problems was proved that they are not solvable in polynomial time.

But there are many important tasks, for which it is very difficult to find a solution, but once we have it, it is easy to check the solution. This fact led to NP-complete problems. NP stands for nondeterministic polynomial and it means that it is possible to "guess" the solution (by some nondeterministic algorithm) and then check it, both in polynomial time. If we had a machine that can guess, we would be able to find a solution in some reasonable time.

Studying of NP-complete problems is for simplicity restricted to the problems, where the answer can be yes or no. Because there are tasks with complicated outputs, a class of problems called NP-hard problems has been introduced. This class is not as limited as class of NP-complete problems.

For NP-problems is characteristic that some simple algorithm to find a solution is obvious at a first sight - just trying all possible solutions. But this algorithm is very slow (usually O(2^n)) and even for a bit bigger instances of the problems it is not usable at all.

Today nobody knows if some faster exact algorithm exists. Proving or disproving this remains as a big task for new researchers (and maybe you! :-)). Today many people think, that such an algorithm does not exist and so they are looking for some alternative methods - example of these methods are genetic algorithms.

Examples of the NP problems are satisfiability problem, travelling salesman problem or knapsack problem. Compendium of NP problems is available.