III. 探索空間(Search Space)

探索空間

私たちがある問題を解決しようとするとき、私たちはいくつかの候補の中で最もよい解を探します。すべての実行できる解の空間(it means objects among those the desired solution is)は、探索空間と呼ばれています。探索空間内の各点が、１つの実行可能な解をあらわしています。どの実行可能な解も、その値または問題に対する適合度で"マーク"されます。私たちは、実行可能な解－つまり探索空間内の点－の中から問題に対する答え１つ（もしくはそれ以上）を探します。

If we are solving some problem, we are usually looking for some solution, which will be the best among others. The space of all feasible solutions (it means objects among those the desired solution is) is called search space (also state space). Each point in the search space represent one feasible solution. Each feasible solution can be "marked" by its value or fitness for the problem. We are looking for our solution, which is one point (or more) among feasible solutions - that is one point in the search space.

解を探すということは、探索空間内のいくつかの極値（最小値、もしくは最大値）を探すことと同じです。

The looking for a solution is then equal to a looking for some extreme (minimum or maximum) in the search space. The search space can be whole known by the time of solving a problem, but usually we know only a few points from it and we are generating other points as the process of finding solution continues.

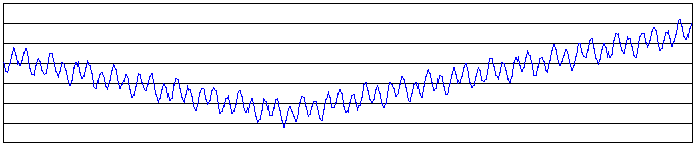
Example of a search space

問題は探索が非常に難しくなりうるということです。１つは探している解がどこにあるのか、またどこから始めればいいのかがわからないということです。いくつかの適切な解(つまり最高の解である必要はないのです)を探す方法、例えばhill climbing,tabu search,simulated anneling,遺伝的アルゴリズムといった、たくさんの方法があります。これらの方法によって見つかった解はしばしば、よい解としてかんがえられます。なぜなら、本当の最適解を証明するのはたいてい可能なことではないのです。

The problem is that the search can be very complicated. One does not know where to look for the solution and where to start. There are many methods, how to find some suitable solution (ie. not necessarily the best solution), for example hill climbing, tabu search, simulated annealing and genetic algorithm. The solution found by this methods is often considered as a good solution, because it is not often possible to prove what is the real optimum.

NP-hard Problems

"伝統的な"方法で解くことのできない難しい問題をＮＰ問題といいます

Example of difficult problems, which cannot be solved int "traditional" way, are NP problems.

There are many tasks for which we know fast (polynomial) algorithms. また、アルゴリズム的に解くことが不可能な問題もあります。そして多項式の時間で解くことができない問題があることが証明されている。

There are many tasks for which we know fast (polynomial) algorithms. There are also some problems that are not possible to be solved algorithmicaly. For some problems was proved that they are not solvable in polynomial time.

But there are many important tasks, for which it is very difficult to find a solution, but once we have it, it is easy to check the solution. This fact led to NP-complete problems. NP stands for nondeterministic polynomial and it means that it is possible to "guess" the solution (by some nondeterministic algorithm) and then check it, both in polynomial time. If we had a machine that can guess, we would be able to find a solution in some reasonable time.

Studying of NP-complete problems is for simplicity restricted to the problems, where the answer can be yes or no. Because there are tasks with complicated outputs, a class of problems called NP-hard problems has been introduced. This class is not as limited as class of NP-complete problems.

NP問題に関して、ちらっと見ただけで明らかに解を見つけることができる単純なアルゴリズムをもっているという特徴があります。それはすべての可能な解を調べることです。しかしこのアルゴリズムは非常に遅いです（普通２のｎ乗のオーダーです、たとえちょっとした問題の例でさえも、そのアルゴリズムは全く使うことができません。）

For NP-problems is characteristic that some simple algorithm to find a solution is obvious at a first sight - just trying all possible solutions. But this algorithm is very slow (usually O(2^n)) and even for a bit bigger instances of the problems it is not usable at all.

今日、より速くて正確なアルゴリズムを知っている人は誰もいません。 Providing or disproviding 新しい研究者（もちろんあなたも! :-) )に対して大きな問題として残っています。しかし、たくさんの人々はそのようなアルゴリズムがあるとは思っていませんそして、彼らは別の方法を探しています。これらの方法の例として遺伝的アルゴリズムがあります。

Today nobody knows if some faster exact algorithm exists. Proving or disproving this remains as a big task for new researchers (and maybe you! :-)). Today many people think, that such an algorithm does not exist and so they are looking for some alternative methods - example of these methods are genetic algorithms.

Examples of the NP problems are satisfiability problem, travelling salesman problem or knapsack problem. Compendium of NP problems is available.